Scaling Law是否失效？清华NLP团队提出Densing Law密度定律，重新定义大模型能力增长

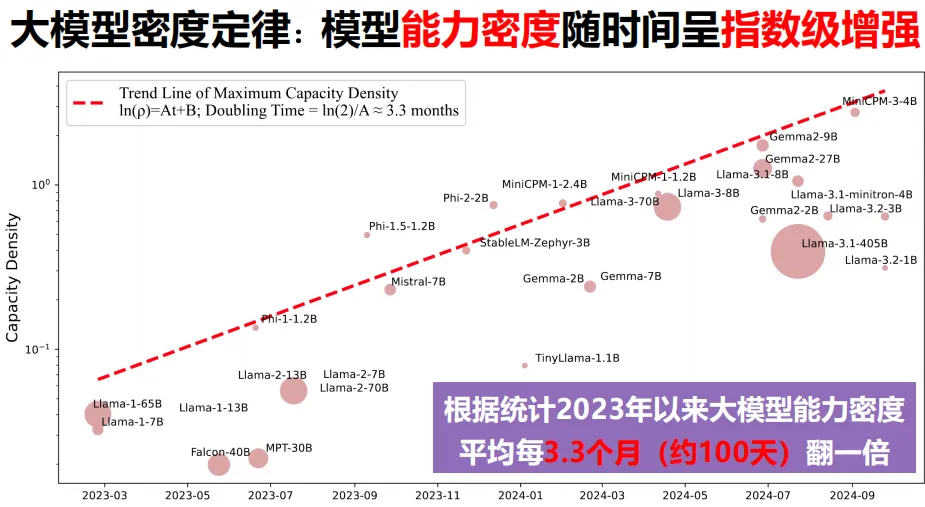
大模型当前颇受瞩目。依照传统的方法，模型性能会随着参数和数据的增加而稳定提升。然而，关于大模型的密度定律，观点各异。它表明，大模型的能力密度大约每100天就会翻一番，这宛如开启了一扇全新的认知之门。

理解密度定律核心

大模型的密度定律与摩尔定律有相似之处。研究团队提出了“有效参数量”与“实际参数量”之比，作为衡量新型大型语言模型训练质量的全新指标。按照这一定律的推算，到明年年底，8B规模的小型模型或许能够达到GPT-4的性能水平。这说明，模型性能的提升并不仅仅取决于规模的增长，这一比值使我们得以重新审视模型的效率。比如在某些应用场景中，如果小模型的有效参数量比值足够高，它们同样可以展现出与大模型相媲美的性能。

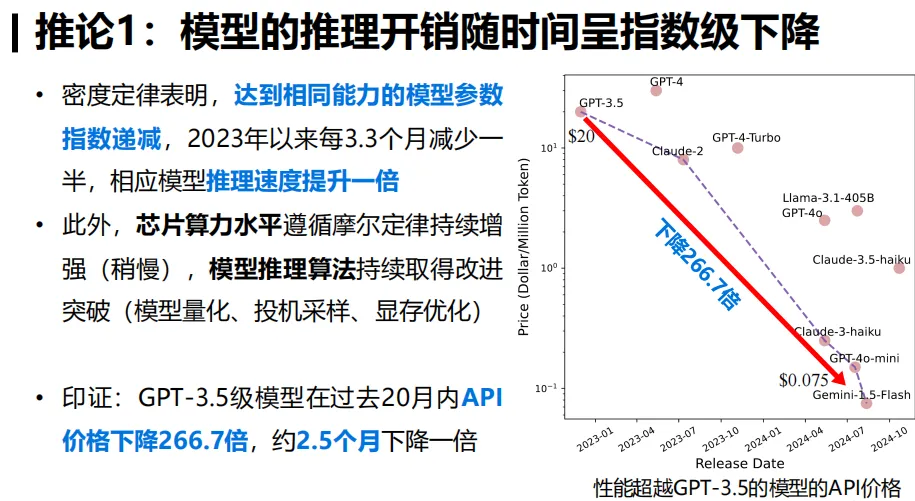
这个定律在时间维度上也有所体现。比如，从2023年1月起至现在，GPT-3.5级模型的推理成本已降至原来的1/266.7。这一变化充分说明了密度定律对模型性能的实际影响极为显著，同时这一数据也揭示了大型模型发展速度之快，令人惊叹。

AI三大核心引擎遵循定律

电力、算力还有人工智能，这三个AI时代的核心动力，都遵循着密度定律，并且各自都有其增长周期。以算力为例，在固定的时间段内，它的增长呈现出一定的规律性。这种规律揭示了整个AI生态系统发展的内在联系。

观察这些关键引擎间的互动，便能领悟到在AI整体框架中，它们正共同进步。这好比电力供应的提升，若能跟上计算能力和智能发展的步伐，便能促进AI产业的迅猛增长。一旦某环节出现问题，比如电力供应短缺，便可能阻碍计算能力和模型智能的发展。

模型“有效期”的影响

模型的有效期限由密度倍增周期决定。数月一更，新型号层出不穷。因此，模型必须在短时间内实现盈利。以新模型为例，若在限定时间内未能积累足够用户或创造足够价值，便可能陷入入不敷出的困境。

新模型的频繁问世给行业带来了持续竞争。开发者们遇到难题，即如何在模型有效期内实现价值最大化。这需要他们综合考虑用户需求、模型适用性等多个方面。

对高效模型压缩算法的需求

研究发现，经过剪枝和蒸馏处理后的模型，其密度比原始模型要低。这一发现推动我们探索更高效的模型压缩技术，尤其是针对小型模型。聚焦于小型模型的研究，若能提高其密度，将显著增强其性能。

在实际应用中，我们可以根据小模型的特性去研究新的压缩技术。比如，针对小模型的架构特点来调整算法，这样做能够增强小模型在执行不同任务时的表现，避免仅仅无目的地增加模型参数。

不要盲目追求Scaling

密度定律警示我们不应盲目追求扩展规模。在模型性能与资源消耗间，需寻求一个恰当的平衡点。尽管Llama-3.1-405B在性能上颇具优势，但其资源消耗却远超其他模型数百倍。

只注重增加模型参数，可能导致发展低效。比如，在大模型在资源有限的小型设备上，可能因为资源消耗过大而无法正常工作。若能处理好效率和性能的平衡，模型便能应用于更广泛的领域。

推理成本的指数下降

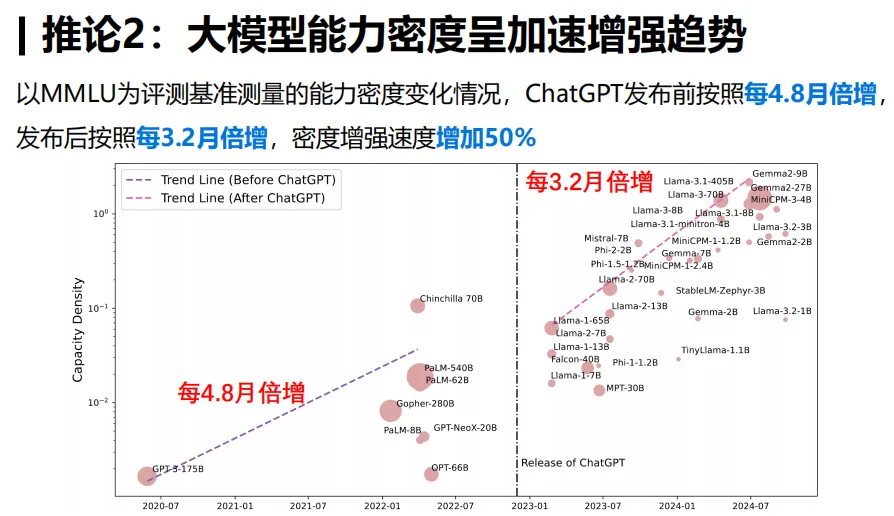
依照密度定律，若要达到相同的任务表现，推理所需成本正以指数形式减少。其原因是，每隔一段时间，我们就能利用参数减半的模型，达到先前模型所具备的性能水平。

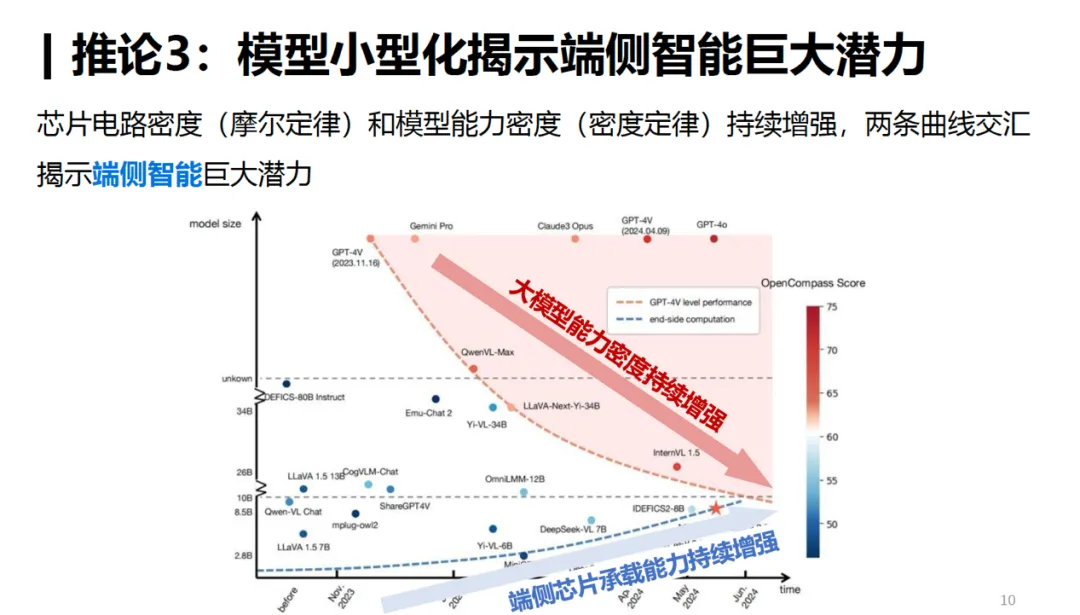
从企业运营成本的角度来看，这对于众多依赖模型提供服务的公司来说是个利好消息。这有助于它们减少硬件投资，提升整体效益。比如，一家初创的人工智能服务企业就能借助这一原则，减少对昂贵硬件的依赖，将资金和资源转向更具价值的研发领域。

在深入了解了众多关于大模型密度定律的知识后，你是否曾思考过，你从事的人工智能业务或研究能否从中得到启发？欢迎大家在评论区留言、点赞和转发。

内容来自网络，如有侵权，联系删除。